Prof. Ricardo Ciani Neto

Número Pi

Mesmo que você não trabalhe com números e as ciências exatas não sejam suas favoritas, tem, no mínimo, uma vaga lembrança do pi. Ele é obtido pela divisão da circunferência de um círculo por seu diâmetro. O resultado é sempre a dízima 3,141592653589793238462643383279502884197169… (e, por aí vai, ela nunca chega ao fim). A data foi estaelecida por causa dos primeiros números (3 = mês de março; 14 = dia).

Fracionando o círculo para calcular a sua área

O número não aparece somente na fórmula do perímetro do círculo. A área do círculo será um conceito que colocará novamente essa constante em uma das fórmulas mais essenciais da matemática.

Essa fórmula é construída fracionando-se o círculo em uma infinidade de triângulos isósceles, sendo que dois lados deverão ter a mesma medida do raio. Além disso, com a preocupação de que esses triângulos sejam iguais, com a medida da base sendo um pequeno segmento do perímetro desse círculo:

Método de cálculo isolado das decimais $π$

Em 1995, David Bailey, em colaboração com Peter Borwein e Simon Plouffe, descobriu uma fórmula de cálculo de π, uma soma infinita(freqüentemente chamada fórmula BBP):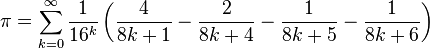 $\pi = \sum_{k = 0}^{\infty} \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6}\right)$

Essa fórmula permite calcular facilmente a enésima decimal binária ou hexadecimal de $π$ sem ter que calcular as decimais precedentes. O sítio de Bailey contém sua derivação e implementação em diversas linguagens de programação. Graças a uma fórmula derivada dafórmula BBP, o 4 000 000 000 000 000° algarismo de $π$ em base 2 foi obtido em 2001.

Grandezas que dependem de $π$

Várias relações matemáticas dependem do conhecimento da constante $π$ , as mais conhecidas a nível didático são:

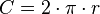
Perímetro de uma circunferência: $C = 2 \cdot \pi \cdot r$
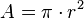
Área do círculo : $A = \pi \cdot r^2$
Volume de uma esfera: $V = {4 \over 3} \cdot \pi \cdot r^3$

$π$ também está nas fórmulas gravitacionais e do eletromagnetismo da física.

Cronologia do cálculo de $π$

Matemático	Ano	Casas Decimais
Egípcios (Papiro de Rhind)	1650 A.C.	1
Arquimedes	250 A.C.	3
Zu Chongzhi	480 D.C.	7
Jamshid Masud Al-Kashi	1424	16
Ludolph van Ceulen	1596	35
Jurij Vega	1794	126
William Shanks	1874	527
Levi B. Smith, John W. Wrench	1949	1.120
Daniel Shanks, John W. Wrench	1961	100.265
Jean Guilloud, M. Bouyer	1973	1.000.000
Yasumasa Kanada, Sayaka Yoshino, Yoshiaki Tamura	1982	16.777.206
Yasumasa Kanada, Yoshiaki Tamura, Yoshinobu Kubo	1987	134.217.700
Chudnovskys	1989	1.011.196.691
Yasumasa Kanada, Daisuke Takahashi	1997	51.539.600.000
Yasumasa Kanada, Daisuke Takahashi	1999	206.158.430.000
Yasumasa Kanada	2002	1.241.100.000.000
Daisuke Takahashi	2009	2.576.980.370.000 ^[14]
Fabrice Bellard	2010	2.699.999.990.000 ^[15]
Shigeru Kondo & Alexander Yee	2010/08/02	5.000.000.000.000 ^[16]